Nonparametric Gaussian Process Covariances via Multidimensional Convolutions

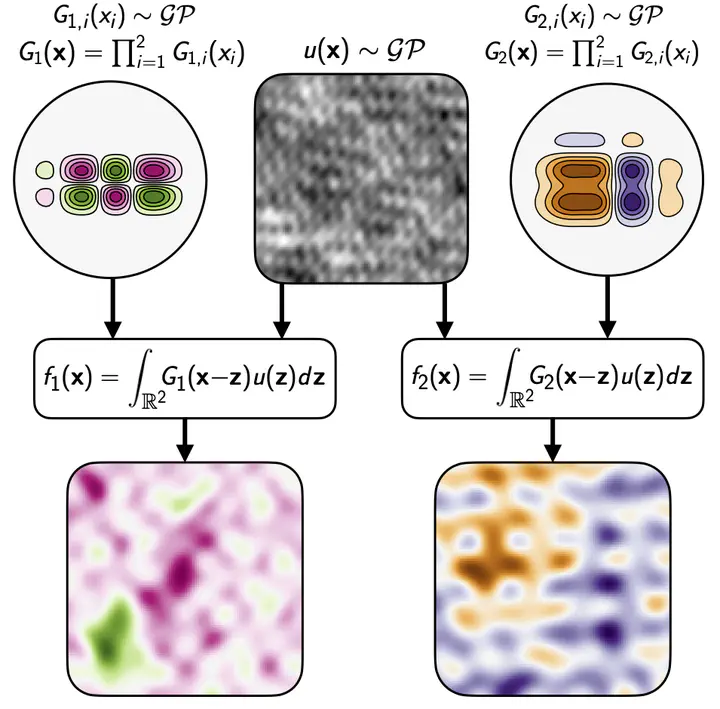
Abstract

A key challenge in the practical application of Gaussian processes (GPs) is selecting a proper covariance function. The process convolutions construction of GPs allows some additional flexibility, but still requires choosing a proper smoothing kernel, which is non-trivial. Previous approaches have built covariance functions by using GP priors over the smoothing kernel, and by extension the covariance, as a way to bypass the need to specify it in advance. However, these models have been limited in several ways: they are restricted to single dimensional inputs, eg time; they only allow modelling of single outputs and they do not scale to large datasets since inference is not straightforward. In this paper, we introduce a nonparametric process convolution formulation for GPs that alleviates these weaknesses. We achieve this using a functional sampling approach based on Matheron’s rule to perform fast sampling using interdomain inducing variables. We test the performance of our model on benchmarks for single output, multi-output and large-scale GP regression, and find that our approach can provide improvements over standard GP models, particularly for larger datasets.